En el fascinante mundo del análisis matemático, comprender la trayectoria de una función es esencial para visualizar su comportamiento y predecir su evolución en diferentes situaciones. En este artículo, exploraremos paso a paso cómo encontrar la trayectoria de una función y la importancia de este concepto en diversas áreas, desde la física hasta la economía.
¿Qué es la trayectoria de una función?
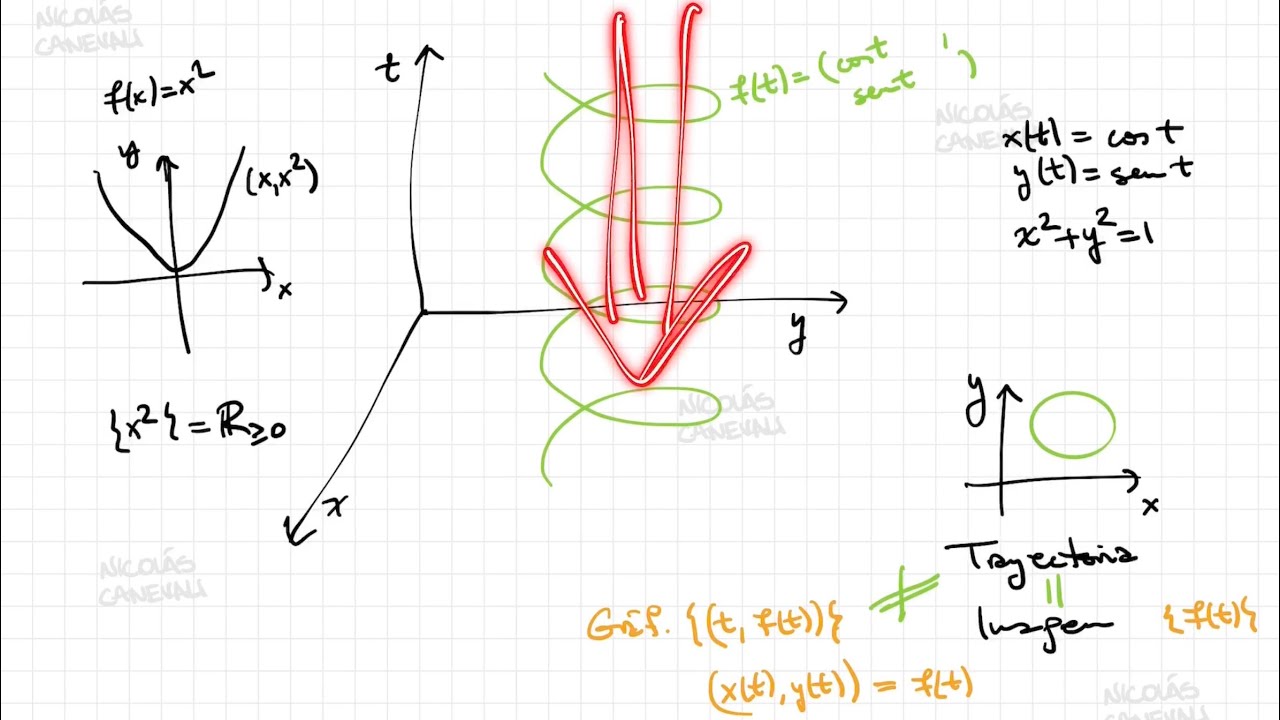
Antes de adentrarnos en los detalles, es crucial comprender qué se entiende por la trayectoria de una función. En términos simples, la trayectoria de una función representa el conjunto de puntos que describe el recorrido de esta función en un espacio determinado. Visualizar esta trayectoria nos permite entender cómo la función se desenvuelve y cómo se relaciona con otras variables.
Pasos para encontrar la trayectoria de una función
Paso 1: Identificar la función
El primer paso es identificar la función de interés. Puede ser una función lineal, cuadrática, exponencial u otra. Por ejemplo, consideremos la función f(x) = x² + 3x – 2 como nuestra función a analizar.
Paso 2: Determinar el intervalo de interés
Es necesario definir el intervalo de interés en el dominio de la función. Este intervalo puede ser crucial para visualizar la trayectoria de manera precisa. Por ejemplo, si queremos analizar la función en el intervalo [0, 5], nos centraremos en ese rango específico.
Paso 3: Calcular la gráfica de la función
Utilizando herramientas matemáticas o software especializado, dibuja la gráfica de la función en el plano cartesiano. Este paso es fundamental para visualizar cómo se comporta la función en el intervalo seleccionado y para identificar posibles puntos de interés como máximos, mínimos o puntos de inflexión.
Paso 4: Analizar la dirección de la trayectoria
Observa la dirección en la que la función se mueve en el plano. ¿La función tiende a crecer o decrecer? Este análisis te ayudará a comprender cómo evoluciona la función en el intervalo definido y cómo se comporta en diferentes puntos críticos.
Importancia de comprender la trayectoria de una función
Una predicción precisa
Entender la trayectoria de una función es fundamental para realizar predicciones precisas en diferentes contextos. Desde la predicción de tendencias económicas hasta la predicción de trayectorias de proyectiles en la física, la capacidad de visualizar cómo una función se desarrolla es invaluable.
Optimización de procesos
En el campo de la ingeniería y la optimización, comprender la trayectoria de una función puede llevar a la mejora de procesos y sistemas. Al identificar puntos críticos y tendencias, los ingenieros pueden optimizar diseños y tomar decisiones informadas.
Interpretación de datos
En el ámbito de la estadística y el análisis de datos, la trayectoria de una función puede ayudar a interpretar de manera más profunda conjuntos de datos complejos. Visualizar cómo una función se relaciona con variables específicas puede revelar patrones ocultos y facilitar la toma de decisiones informadas.
¿La trayectoria de una función siempre es una línea recta?
En realidad, la trayectoria de una función no necesariamente es una línea recta. Puede tomar diversas formas, desde curvas suaves hasta líneas rectas, dependiendo de la naturaleza de la función en cuestión y su comportamiento en el espacio.
¿Cómo influyen los puntos críticos en la trayectoria de una función?
Los puntos críticos, como los máximos, mínimos y puntos de inflexión, juegan un papel crucial en la trayectoria de una función. Estos puntos pueden indicar cambios significativos en la dirección de la función y ayudar a comprender su comportamiento global.